Aunque parezca un contenido trivial y muy principiante, el trabajo con arrays dentro de python, constituye parte fundamental para el análisis de datos en este lenguaje de programación. En esta entrada pretendemos recoger diferentes funciones que nos permiten crear matrices en python, usando la librería Numpy.
Podemos hacerlo de la siguiente manera:

Primeramente Importamos la librería numpy python, luego creamos el array de la dimensión que queramos
Crear matrices a partir de listas
También podemos crear arrays a partir de listas ya creadas, por ejemplo:

matriz de ceros
Para inicializar un array cuyos elementos sean 0, tenemos una función en numpy que nos facilita la vida:

matriz de unos
También podemos inicializar un array donde todos los elementos sean la unidad:

np.repeat()
Una función que sirve para generalizar los dos ejemplos enteriores es np.repeat(), donde podemos inicializar una matriz donde todos sus elementos sean iguales:

Matriz identidad
En matemáticas, llamamos matriz identidad a una matriz cuyos todos elementos son 0, menos los de su diagonal principal que son 1. En álgebra matricial se le denomina elemento neutro en el producto vectorial.

El código compartido son capturas de pantalla. El secreto no está en copiar y pegar código, sino en entenderlo.
Creando una matriz a partir de un intervalo
Este tipo de matriz la vamos a utilizar muchísimo:


Si solo le pasamos un solo parámetro, empezará desde el 0 hasta el número dado (solo con números naturales):

numpy.shape
Me devuelve las dimensiones del array.

numpy.dtype
Nos dice el tipo de elementos que tiene el array

numpy.reshape()
Redimensiona el array.

Matrices y escalares
En versiones antiguas de python, la operación 5/2, nos devuelve un valor entero ya que 5 y 2 son enteros, que lo que hace es truncar el resultado de esta operación, por tanto me devolvería un 2. Para evitar esto podríamos declarar que uno de los dividendos es float, 5./2 y por tanto si me devolvería un float, o sea 2.5. Esta cuestión no ocurre a partir de python 3. Otra solución podría ser la siguiente:
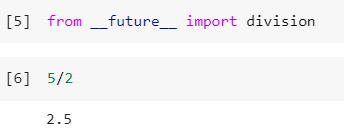
Operaciones entre dos matrices
Podemos operar con dos matrices si tienen las mismas dimensiones (igual shape) y se operaría (sumando, restando, multiplicando, dividiendo, etc) el elemento del primer array con el elemento correspondiente del segundo array. No confundir con el producto de matrices que lo podemos ver más abajo. En el siguiente ejemplo podemos ver dos arrays, y el resultado de la operación arr1*arr2 y arr1+arr2 .


También podemos sumar de la siguiente manera:

Más abajo podrás encontrar más funciones que nos permiten operar entre dos matrices:
También podemos operar una matriz con un escalar, y se operaría el escalar con cada elemento del array.
Por ejemplo:
np.append()
Con esta función podemos unir dos matrices en una, por ejemplo:

Generando matrices con datos aleatorios
Es muy común que necesitemos inicializar una matriz con datos aleatorios, y es tan sencillo como esto:

Tener en cuenta, que np.random.randn() genera números aleatorios dentro de una distribución normal. Si lo que queréis es generar números aleatorios uniformes, donde todos los números tengan la misma probabilidad de salir puedes usar np.random.uniforme():

Como podéis ver en el ejemplo anterior x_shape representa las dimensiones que queremos que tenga la matriz generada.
Volviendo a np.random.randn(), ayudándonos de la función reshape, podemos modificar la dimensión esa matriz según queramos, aunque la misma función np.random.randn() nos lo puede hacer:

np.argmax()
Esta función nos devuelve el índice del elemento que tenga el máximo valor:

np.random.shuffle()
Cuando estamos preparando datos para utilizarlo como entrenamiento de modelo de inteligencia artificial, es muy útil desordenar los datos, para evitar influencia en el orden de los datos, numpy tiene una función que nos desordena los elementos de un array:

Indexando matrices
Podemos llamar a un elemento con el indice específico de un array de la siguiente manera:

También puedo obtener los valores de un rango en particular, por ejemplo :

Como podrás ver en el ejemplo anterior, hemos llamado a todos los elementos cuyo indice están entre a y b, donde a está incluído pero no b, por tanto si llamamos a todos los elementos entre 4 y 9, nos devolverá el 4, 5, 6, 7 y 8.
Como complemento al ejemplo anterior, si al consultar un rango dejamos en blanco a o b, nos hace lo siguiente:

También puedo cambiar los valores de los elementos del array, por ejemplo:

Por supuesto podemos crear un nuevo array a partir de un conjunto de elementos de otro array ( seguir leyendo ya que hay una particularidad):

Por supuesto podemos modificar los valores de este nuevo array:

Hasta aquí todo bien, pero vamos ahora a consultar el array original:

¿¿¿¿PERO SI NO HE MODIFICADO EL ARRAY ORIGINAL POR QUE CAMBIA?
Lo que ocurre es que en numpy no se copia el array, simplemente hace una vista del array original, de esta manera no tenemos varias copias de la matriz dando vueltas por ahí, por tanto cualquier cambio en una de las vistas modifica el array original.
Para crear una copia lo tenemos que hacer de la siguiente manera:

Al crear el subArray usamos .copy() y ya no me hace una vista del array original, sino que me hace una copia, por tanto cualquier modificación en subArray no modifica el array original.
Indexando matrices en 2D
Podemos crear arrays en 2D con numpy de la siguiente manera:

y podemos consultar los valores llamando a sus índices:

Una forma de interpretar esto es ver que tenemos un array donde sus elementos son arrays. En el ejemplo anterior tenemos un array de 3 elementos, donde cada elemento es a su vez un array con 3 elementos, por tanto, imaginaros que quiero consultar el segundo elemento del array principal, pues simplemente consulto array[1] y me devolverá el array que hay en ese elemento, si ahora quiero acceder al segundo elemento de ese array que he consultado lo hago así array[1][2], como se puede ver en el final del ejemplo anterior.
De igual manera a como lo hacíamos en un array de una dimensión, podemos cambiar los valores de un array 2D:

También podemos consultar, obtener o copiar un subconjunto del array principal, por ejemplo quiero obtener un array 2×2 desde la esquina inferior derecha, que correspondería a la segunda y tercera fila y segunda y tercera columna:

Transposición de matrices con numpy
La transposición de arrays es muy utilizado en el modelado de datos, si tenéis dudas podéis ver más información aquí.
Usando la librería de numpy en python es tan sencillo como:

Transponer matrices en 3 dimensiones
Si queremos transponer un array con 3 dimensiones lo podemos hacer así:

Aunque la mejor manera y generalmente la más usada es con np.swapaxes()
np.swapaxes()
Con esta función simplemente tenemos que especificar entre que ejes queremos realizar la transposición.
Tomando el ejemplo anterior donde creamos un array 3D con las dimensiones 4 x 3 x 2, donde tenemos un array de 4 filas, con 3 columnas, donde cada elemento es a su vez un array de dos elementos, el eje 0 es el de las filas o sea 4, el eje 1 es el de las columnas, o sea el 3, y el eje 2 es del array de 2 elementos que hay en casa elemento de la matriz principal.
Por ejemplo si quieremos hacer una transposición exactamente como el ejemplo anterior, tendriamos que transponer los ejes 0 y 1. Veámoslo con código:

Si hacemos la transposición entre el eje 1 y 2 quedaría así:

y por último si transponemos entre el eje 0 y 2 quedaría así:

Producto de matrices con python (numpy)
Podemos hacer el producto de matrices de la siguiente manera:

Funciones universales en matrices con numpy
Podemos aplicar funciones matemáticas conocidas directamente a una matriz con numpy sin necesidad de recorrer el array, veamos algunos ejemplos:
np.sqrt()

np.exp()

np.maximum()
Me compara cada elemento de los dos arrays y me devuelve un array con el mayor de cada elemento.

np.minimum()
Lo mismo que np.maximum() pero con el mínimo

Podéis encontrar muchísimas más funciones universales como estas aquí:
https://docs.scipy.org/doc/numpy/reference/ufuncs.html#available-ufuncs
Guardar y cargar matrices con numpy en python
Podemos con numpy guardar uno o varios arrays en un archivo externo. Veamos varios ejemplos:

Aquí hemos guardado arr creado inicialmente en un archivo firstArray.npy y luego lo hemos cargado.
Si queremos hacer lo mismo pero con varios arrays, creamos un fichero .npz de la siguiente manera:

Guardar matrices en .txt con numpy
También podemos guardar y cargar los arrays de numpy en un archivo .txt para utilizarlos con otro programa, de la siguiente manera:

