Funciones de activación redes neuronales artificiales

Las funciones de activación son otro pilar fundamental para el desarrollo de modelos de aprendizaje automático.

¿Qué hace la función de activación en redes neuronales?

La función de activación de una neurona, nos define la lógica necesaria para activar o no la neurona ante una entrada de datos, relacionando los pesos de la neurona y el umbral de excitación.

Para utilizar en nuestros modelos las funciones de activación de TensorFlow tenemos que importar lo siguiente:

Ahora veamos algunas funciones de activación interesantes y más usadas.

Función de activación ReLU en TensorFlow

ReLU es una de las funciones más utilizadas para introducir una no linealidad en la red neuronal. Aunque luego la veremos gráficamente es interesante saber que esta función se define como:

o sea:

ReLU = max(0, x)

esto quiere decir introducimos un número en esta función nos devuelve el mismo número siempre que sea mayor que 0, en el caso que ese número sea menor o igual que 0, nos devolverá un 0.

Si queréis conocer más sobre esta función podéis ir aquí.

Veamos algún ejemplo con código:

Como podéis ver cuando los inputs son negativos, ReLU nos devuelve 0, y cuando es mayor que 0, nos devuelve el mismo input.

Vamos a añadir algunas líneas más para visualizar estos puntos en una gráfica. No os preocupéis si no entendéis las últimas líneas, ya haremos una serie esto más adelante.

Función de activación ReLU6

Podemos usar la función ReLU6, que es computacionalmente más rápida. Esta función se define como:

ReLU6 = min(max(0, 6), 6)

Veámosla con un poco de código y como se dibuja:

Como podemos ver para inputs menores que 6 se comporta como una ReLU, y para inputs mayores que 6, nos devuelve 6.

Función de activación sigmoide

La función sigmoide es una de las más utilizadas como función de activación, y podemos definirla como:

sigmoide = 1 / (1 + exp (-x))

Usarla con mucha precausión ya que con redes neuronales muy densas puede dar problemas de optimización.

Como podemos ver, siempre nos devuelve valores entre 0 y 1.

Debemos tener en cuenta que algunas funciones de activación no están centradas en cero, como la sigmoide. Esto requerirá que hagamos cero a los datos antes de usarlos en la mayoría de los algoritmos de gráficos computacionales

La tangente hiperbólica como función de activación

La tangente hiperbólica se parece mucho a la sigmoide, pero ésta nos devuelve valores entre -1 y 1.

o sea:

Podemos verlo con código:

Softsign. Funciones de activación

Definimos la softsign como:

softsign = x / (abs(x) + 1)

Veámosla con código:

Función de activación Softplus

Softplus es otra función de activación que la podemos definir como:

y en código es:

ELU Función de activación

Aunque hay más funciones de activación vamos a ver dos últimas funciones de activación, una de ellas es la función ELU.

La podemos definir como:

Y con código sería así.

Softmax

Aquí tenemos otra función de activación, la cual se define como:

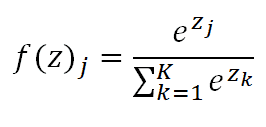
Al implementarlo en código quedaría así:

Resumiendo funciones de activación

Veamos un resumen de las funciones que hemos visto anteriormente con código y al final generaremos una gráfica comparando cada función:

y se vería así: