Concepto de conjunto
Un conjunto es básicamente un grupo de cosas que comparten una o más características en común.
Piensa en un conjunto como una colección de elementos. Un conjunto está bien definido cuando podemos señalar y decir qué cosas están en él.
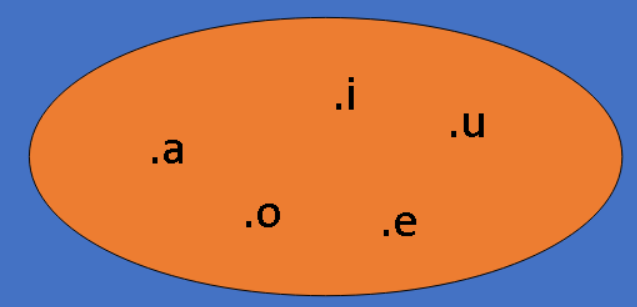
Por ejemplo, considera el conjunto de vocales, que son las letras a, e, i, o y u. Lo interesante aquí es que todas estas letras tienen en común ser vocales.
También podemos tener conjuntos más complicados, como los puntos que forman un círculo con centro en P y radio r, o los estudiantes en una clase, o los colores que aparecen en un arcoíris. Incluso podemos tener conjuntos de números como los impares o los enteros menores que 100.
Para escribir un conjunto, usamos letras grandes y ponemos los elementos dentro de llaves. Así que, si tenemos un conjunto llamado A que contiene los números pares menores que 10, se vería así:
A = {2, 4, 6, 8}.
Los elementos están separados por comas.
Si queremos hablar del conjunto de días de la semana, lo llamaremos W y escribiremos:
W = {lunes, martes, miércoles, jueves, viernes, sábado, domingo}
Y para el conjunto de vocales, tendríamos:
V = {o, a, e, i, u}
Pensemos en el conjunto de las primeras 5 letras del alfabeto:
A = {a, b, c, d, e}
Ahora, para el conjunto de potencias de 10 (números enteros y positivos), lo expresaríamos así:
K = {10n, n ∈ N}
A menudo, es útil visualizar conjuntos usando diagramas para entender mejor sus definiciones y propiedades. Los diagramas de Venn, inventados por John Venn alrededor de 1880, son representaciones gráficas donde los elementos del conjunto se marcan como puntos dentro de regiones cerradas.
Ok, echemos un vistazo a las diferentes formas de definir conjuntos:
a) Vamos a hablar primero de la definición POR EXTENSIÓN. Básicamente, aquí listamos todos los elementos del conjunto uno por uno. Por ejemplo, consideremos el conjunto Z compuesto por los elementos a, b, c, d y e. Para definir este conjunto por extensión, lo anotamos así:
Z = {a, b, c, d, e}
Otro ejemplo es el conjunto de vocales, V:
V = {a, e, o, i, u}
Oh, y un conjunto unitario es aquel con solo un elemento. ¿Ejemplo? Claro, el conjunto {p}.
b) Ahora, hablemos de la definición POR COMPRENSIÓN. Aquí, en lugar de enumerar los elementos, describimos la propiedad que todos comparten. Digamos que tenemos el conjunto S de números primos menores que 20:
S = {números primos menores que 20}
Y podríamos expresarlo como:
S = {X | X es un número primo menor que 20}
La idea es: «S es el conjunto de los números X tales que X es un número primo menor que 20«.
También, tenemos otro conjunto B, con elementos a, b y c. Podemos definirlo por comprensión así:
B = {las tres primeras letras del alfabeto}
Usamos esta forma cuando listar los elementos uno por uno se vuelve engorroso. Imagina definir el conjunto de reptiles, sería un rollo enumerarlos, ¿verdad? Así que usamos la definición por comprensión.
Si llamamos R al conjunto de reptiles, la definición se ve así:
R = {animales reptiles}
Es interesante notar que tanto la definición por extensión como la definición por comprensión evitan tener que definir un conjunto verdaderamente. Es decir, un conjunto no es algo que puedas realmente definir completamente.
Estos conceptos básicos, como conjunto, elemento y pertenencia, son ideas intuitivas que aceptamos y en las que basamos la nueva matemática. Las tomamos como verdades básicas y construimos a partir de ellas, de la misma forma en que en geometría euclidiana partimos de axiomas para desarrollar la geometría tradicional.
Relación de pertenencia de un conjunto
Básicamente, esta relación nos dice si un elemento está o no dentro de un conjunto. Para decir que un elemento está en un conjunto, usamos el símbolo ∈, que significa «pertenece a».
Por ejemplo, si tenemos a ∈ A, eso simplemente significa que el elemento a está en el conjunto A.
Ahora, si queremos decir que un elemento no está en un conjunto, utilizamos el símbolo ∉, que básicamente dice «no pertenece a».
Supongamos que F es el conjunto de vocales. Si queremos dejar claro que la letra b no es parte de ese conjunto, lo escribimos así:
b ∉ F
De esta manera estamos diciendo que la letra b no pertenece al conjunto F.
Conjunto complementario y conjunto vacío
Cuando tenemos dos conjuntos A y B, con B conteniendo a A, el conjunto complementario de A con respecto a B es simplemente el conjunto de elementos en B que no están en A.
Para representar este conjunto complementario, usamos varios símbolos que son equivalentes:
- Ā
- A’
- CBA
Todos estos simbolizan lo mismo: «conjunto complementario de A». En el tercer símbolo, además, se especifica con respecto a qué conjunto es complementario.
Ahora, vamos a poner esto en acción con dos conjuntos:
Digamos que tenemos A = {1, 2, 3} y B = {1, 2, 3, 4, 5, 6}.
El conjunto complementario de A con respecto a B sería el conjunto de elementos en B que no están en A, es decir, los elementos 4, 5 y 6.
Si usamos los símbolos que mencioné antes, quedaría así:
Ā = A’ = CBA = {4, 5, 6}
En la siguiente figura puede verse la representación gráfica mediante diagramas de Venn del conjunto complementario.
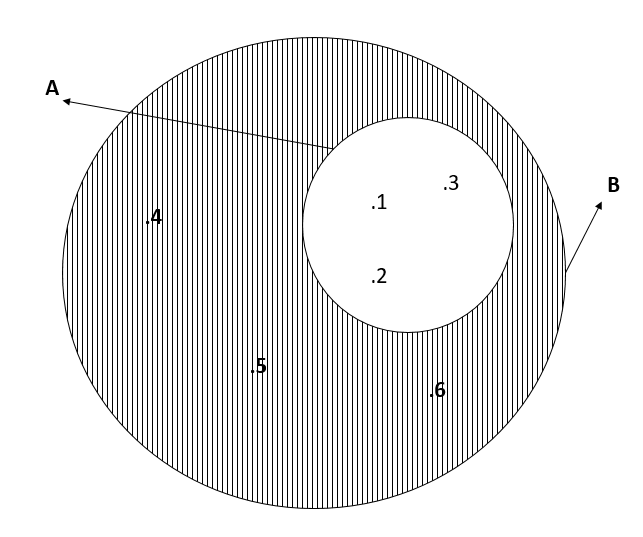
La parte rayada corresponde al conjunto complementario de A con respecto a B.
Imagina que tenemos tres conjuntos: K, que contiene todas las letras; C, que tiene las consonantes; y V, que alberga las vocales. Al observar, encontramos que:
Conjunto de Consonantes de K, o sea CKC = V
Ahora, hablemos del conjunto vacío. Este es aquel que simplemente no tiene nada adentro, como un casillero sin objetos. Usamos el símbolo ø para representarlo. En cierta forma, es un conjunto «límite», un poco como el fin del espectro.
Por ejemplo, considera el conjunto de elementos que son pares e impares a la vez. Pues bien, este conjunto vacío, porque no hay ningún elemento que pueda ser simultáneamente par e impar. Imagina tratar de encontrar un número así, ¡no lo encontrarás!
Otro caso, si pensamos en el conjunto de números que son menores que 7 y al mismo tiempo mayores que 15. ¡Pues sí, también estamos frente a un conjunto vacío! No existe número alguno que se ajuste a ambas condiciones a la vez.
En resumen, el conjunto vacío es un concepto interesante, representa la ausencia total de elementos y se presenta en situaciones donde no podemos encontrar un elemento que cumpla ciertas propiedades al mismo tiempo.
