Relación de inclusión
Consideremos el escenario de conjuntos. En dicho contexto, postulamos que un conjunto, denominado A, está completamente contenido en otro conjunto, designado como B, si cada uno de los elementos que constituye A es simultáneamente un elemento que pertenece a B.
Para denotar esta relación de contención, adoptamos la notación A ⊂ B, la cual se interpreta como «A está contenido en B». Alternativamente, se puede expresar como «A está incluido en B», o también como «B contiene a A».
Para ilustrar este concepto, tomemos dos conjuntos: A = {a, b, c} y B = {a, b, c, d, e}. Efectuando un análisis, se evidencia que la totalidad de los elementos que conforman A también forman parte de B. Por ende, podemos concluir que A ⊂ B. Lo podemos ver en el siguiente diagrama de Venn.
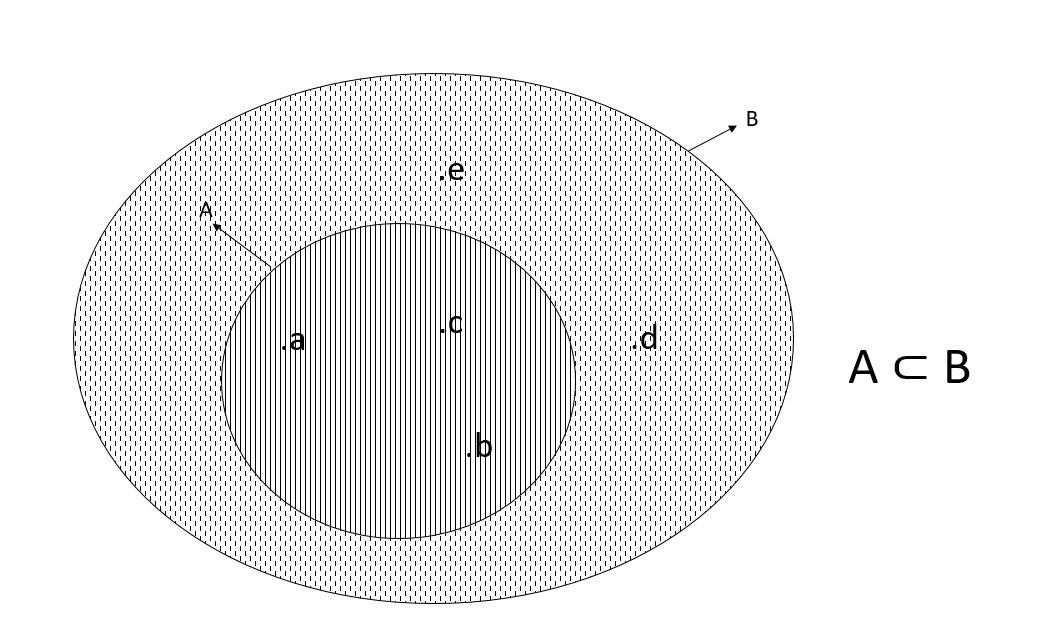
Cuando surge la necesidad de manifestar la no inclusión del conjunto A en otro conjunto B, se recurre al símbolo ⊄, cuya interpretación es «no está contenido en».
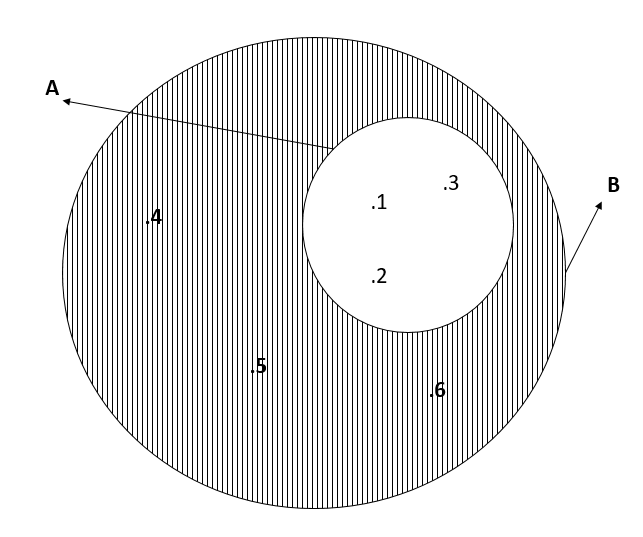
Tomemos en consideración el siguiente caso ilustrativo: consideremos los conjuntos A = {1, 2, 3, 4} y B = {3, 4, 5, 6}. Dado que no se verifica la condición de que todos los elementos del conjunto A sean elementos del conjunto B, es válido afirmar que el conjunto A no está contenido en el conjunto B. Esta afirmación se plasma en la expresión matemática:
A ⊄ B
Esto puede verse claramente en el siguiente diagrama de Venn.

Consideremos B como el conjunto que engloba las vocales y L como el conjunto que agrupa las letras del alfabeto. En consecuencia, podemos establecer la relación:
B ⊂ L
Esta notación, B ⊂ L, denota que el conjunto B es un subconjunto de L, lo cual significa que cada vocal contenida en B es también una letra perteneciente a L.
En términos generales, un conjunto X es considerado un subconjunto de otro conjunto Y si cada elemento que forma parte de X es también un elemento de Y. Es relevante apreciar esta definición en su sentido más amplio, lo que implica que cualquier conjunto es considerado como un subconjunto de sí mismo:
Y ⊂ Y
En la siguiente figura podemos ver cómo el conjunto A = {1, 2, 3} al estar incluido en el B = {1, 2, 3, 4, 5, 6}, es subconjunto de él:
Consideramos el concepto de conjunto potencia, denotado por P, seguido de la notación entre paréntesis que identifica al conjunto en cuestión. Este conjunto potencia se define como el conjunto que engloba todas las posibles agrupaciones más pequeñas que pueden ser construidas a partir de los elementos del conjunto original.
Dado un conjunto C = {a, b, c}, el conjunto potencia P(C) asociado a C está compuesto de la siguiente manera:
P(C) = {ø, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}
Es relevante notar que los elementos pertenecientes al conjunto P(C) representan la totalidad de las combinaciones subconjuntistas factibles derivadas del conjunto C original.
Igualdad de conjuntos
Dos conjuntos A y B se consideran iguales, denotado como A = B, si y solo si ambos conjuntos contienen exactamente los mismos elementos. Esto significa que cada elemento en A también está en B, y cada elemento en B también está en A.
Tomemos los conjuntos: A = {1, 2, 3, 4} y B = {1, 2, 3, 4}
En este caso, A = B, porque todos los números en A también se encuentran en B, y viceversa.
Si A representa el conjunto de provincias de Galicia y B contiene las provincias {A Coruña, Pontevedra, Ourense, Lugo}, entonces A = B, ya que todas las provincias en A también están presentes en B y viceversa.
Consideremos los conjuntos: A = {a, b, c, d} y B = {a, e, i, o, u}
Aquí, A ≠ B, porque aunque comparten el elemento «a», hay otros elementos en B (como e, i, o y u) que no están en A. Por lo tanto, A y B no son iguales.
